Вывод

За пределами 'Hello World': алгоритмы сортировки в Rust

Перевод | Автор оригинала: Matt Oswalt

В этом году я использовал Rust не только как новую возможность для обучения, но и как услугу для нескольких побочных проектов, в которых я принимал участие.

Как и многие разработчики, я учусь на собственном опыте. Проведя несколько недель за чтением книги Rust и просмотром видеороликов, я стал искать несколько простых идей для проектов, которые я мог бы использовать для изучения языка, который идет дальше простого «Hello World», который часто на самом деле не дает вам большого разнообразия. .

Друг предположил, что полезным проектом может быть реализация некоторых популярных алгоритмов сортировки. Это показалось мне действительно удобным инструментом при изучении любого языка. В зависимости от того, на что вы смотрите, вам нужно будет выйти за рамки простых операторов печати и перейти к итерации, рекурсии, функциям, определениям типов и, возможно, многому другому.

Это может не охватывать даже половины языковых функций, но это определенно лучшее введение, чем просто вывод текста на экран.

Кроме того, прежде чем мы начнем: это не предназначено для начинающих по алгоритмам. В любом случае я попытался сделать это несколько лет назад, но также есть огромное количество других бесплатных ресурсов по этому поводу. Вместо этого, это быстрое исследование того, как я реализовал несколько распространенных примеров в Rust, и краткое изложение того, что я узнал о языке в процессе.

Перейдите в мой репозиторий GitHub, если вы хотите увидеть (или запустить) готовую работу из приведенных ниже упражнений.

Пузырьковая сортировка

Большинство курсов по алгоритмам начинаются с «пузырьковой сортировки». Напомню, что этот алгоритм работает путем итерации по массиву значений, меняя местами любую пару значений, которые не соответствуют порядку. Конечно, за один проход с первого раза вряд ли можно будет отсортировать весь массив, поэтому эта итерация повторяется снова и снова, пока массив не будет отсортирован. Из-за этих вложенных циклов пузырьковая сортировка работает с временной сложностью O (n ^ 2), что довольно плохо. Тем не менее, это простой пример для начала, который хорошо показывает влияние плохо оптимизированного алгоритма.

Давайте попробуем это сделать в Rust.

Моя первая попытка была довольно дерьмовой. Он успешно реализовал алгоритм пузырьковой сортировки, но сразу же я обнаружил, что борюсь с концепцией заимствования Rust (которую я все еще пытаюсь понять), а также с тем, что нельзя / нельзя изменять. Исходя из моего опыта работы с Go и Python, моим «по умолчанию», когда дело доходит до циклов, является цикл «for», поэтому я попытался использовать его здесь.

Это решение имело неприятный волновой эффект, который заставил меня принять другие плохие решения только для того, чтобы код скомпилировался:

Внесение изменений в вектор во время итерации по нему было невозможно, поэтому я создал vec_mut с помощью функции vec.to_vec(), создав изменяемую копию. Изначально я разместил это в верхней части функции, вне цикла.
Создание vec_mut вне цикла дало мне ошибку «значение перемещено», о которой я расскажу ниже. Единственный способ заставить это работать - это переместить это внутрь цикла, что, очевидно, неэффективно и бессмысленно, но это сработало.
Изначально я объявил vec, входной параметр этой функции, неизменяемым (просто vec: Vec). Причина, по которой я создавал эту копию, заключалась в том, чтобы иметь изменяемую копию, на которой я мог бы менять местами элементы. Я надеялся, что смогу вернуть vec_mut из этой функции, но это было невозможно, потому что, как упоминалось выше, это должно было быть объявлено внутри функции и было недоступно за пределами этой области. Это означало, что мне пришлось сделать vec = vec_mut;, что, конечно же, означало, что vec должен быть изменяемым (оглядываясь назад, я, вероятно, мог бы вернуть vec_mut из внешнего цикла вместо того, чтобы ломаться, но это имеет свои проблемы и является моя любимая мозоль).

Фу. Вот функциональный, но уродливый результат во всей красе:

fn bubble_sort(mut vec: Vec<i32>) -> Vec<i32> {

    loop {

        // We can't change items of a vector while iterating, so let's create
        // a copy of it first, and we'll make changes here while iterating over
        // the immutable original
        let mut vec_mut = vec.to_vec();

        let mut swapped = false;

        let mut i = 0;
        for _item in vec.iter() {
            if i >= vec.len()-1 { break; }

            if vec[i] > vec[i+1] {
                swapped = true;
                let value = vec[i];
                vec_mut.remove(i);
                vec_mut.insert(i+1, value);
                break;
            }
            i += 1;
        }

        vec = vec_mut;

        // no swaps? Then we're sorted
        if !swapped { break; }
    }

    vec
}

Как упоминалось выше, создание копии vec_mut вне цикла оказалось невозможным, поскольку компилятор выдавал мне следующие ошибки:

RUST_BACKTRACE=1 cargo run --example bubblesort
   Compiling rust-algorithms v0.1.0 (/home/mierdin/Code/rust-algorithms)
error[E0382]: borrow of moved value: `vec_mut`
  --> examples/bubblesort.rs:36:17
   |
20 |     let mut vec_mut = vec.to_vec();
   |         ----------- move occurs because `vec_mut` has type `std::vec::Vec<i32>`, which does not implement the `Copy` trait
...
36 |                 vec_mut.remove(i);
   |                 ^^^^^^^ value borrowed here after move
...
43 |         vec = vec_mut;
   |               ------- value moved here, in previous iteration of loop

Из-за того, что я возвращал vec_mut к vec, я передал право владения значением vec вместо того, чтобы делать копию. Это означало, что на следующей итерации цикла я больше не мог удалять значения из vec_mut. Если бы я хотел, я мог бы сделать еще одну копию с vec = vec_mut.to_vec(); вместо этого, но потом я делаю копии с копий, а это уже выходит из-под контроля. Технически это также происходило, когда у меня было создание vec_mut во внешнем цикле, но в этом случае право собственности было повторно установлено, и я смог снова удалить значения из него, поэтому это сработало. Это маскировало мои плохие права собственности.

Итак, теперь я уверен, что убедил вас, что я способен писать плохой Rust. Давайте двигаться дальше.

Простое использование цикла while со счетчиком немного упрощает ситуацию. Я знаю, что во многих случаях использование цикла for, как и раньше, помогает избежать таких вещей, как ошибки выхода за границы индекса, но в данном случае я думаю, что простота стоит того. При этом мне все равно нужно передать vec как изменяемый, но, поскольку я не повторяю его, я могу выполнить необходимые замены напрямую и вернуть результат по завершении.

fn bubble_sort(mut vec: Vec<i32>) -> Vec<i32> {
    loop {
        // Default to false, so we know by the end if we had any swaps,
        // which indicates we need to do another pass
        let mut swapped = false;
        
        // Iterate over the length of vec, swapping any values that are out of order.
        let mut i = 0;
        while i < vec.len() {
            if i >= vec.len()-1 { break; }
            if vec[i] > vec[i+1] {
                swapped = true;
                let value = vec[i];
                vec.remove(i);
                vec.insert(i+1, value);
                break;
            }
            i += 1;
        }

        // no swaps? Then we're sorted, and we can exit and return the final `vec`
        if !swapped { break; }
    }

    vec
}

Реализация этого алгоритма дала мне реальный, Rust опыт работы с:

Векторы
Итераторы
Заимствование

Неплохо для одного из простейших алгоритмов сортировки. Давайте перейдем к чему-то более сложному (и эффективному).

Сортировка слиянием

Я также хотел заняться «сортировкой слиянием», в основном потому, что это один из моих любимых. Помимо того, что она намного эффективнее пузырьковой сортировки, мне нравится ее принцип работы.

«Разделяй и властвуй» природа сортировки слиянием означает, что мы используем рекурсию для разделения задачи на все меньшие и меньшие подмассивы до такой степени, что они имеют только один элемент и, следовательно, сортируются. Создание окончательного отсортированного массива сводится к объединению этих меньших массивов в более крупные, пока, наконец, у нас не будет один большой отсортированный массив того же размера, что и несортированный, с которого мы начали. Объединение этих подмассивов выполняется путем взятия меньшего значения из начала каждого массива и продвижения по ним до тех пор, пока не останется больше значений.

Я думаю, что это то, что мне нравится в сортировке слиянием - мы разбираем проблему до тех пор, пока фундаментальная истина не становится неизбежной (что два массива отсортированы), и мы снова объединяем их вместе, используя процесс, который эксплуатирует и полностью основан на этой истине. Я всегда считал, что это очень элегантный и даже красивый способ решения проблемы.

В любом случае, независимо от языка, первое, что вам нужно сделать, это определить, имеет ли входящий массив (в нашем случае вектор) только один элемент. Если так, мы можем вернуться сразу же, потому что делить больше нечего; в этот момент пора побеждать.

// If we're already down to the atomic level, return right away
if vec.len() == 1 {
  return vec;
}

Предполагая, что мы прошли мимо этого, мы знаем, что наш вектор содержит как минимум два элемента, что означает, что мы можем разделить его на два «подвектора» как часть «разделяющей» части нашей стратегии.

Я объявил, что d устанавливается равным результату деления длины нашего входного вектора vec на 2. Частное для этой операции является целым числом, которое было закрыто, что означает, что если был остаток, он отбрасывается, и мы остаемся с меньшим целым значением. Итак, если наша длина 4, d равно 2. Если длина 5, d все равно 2.

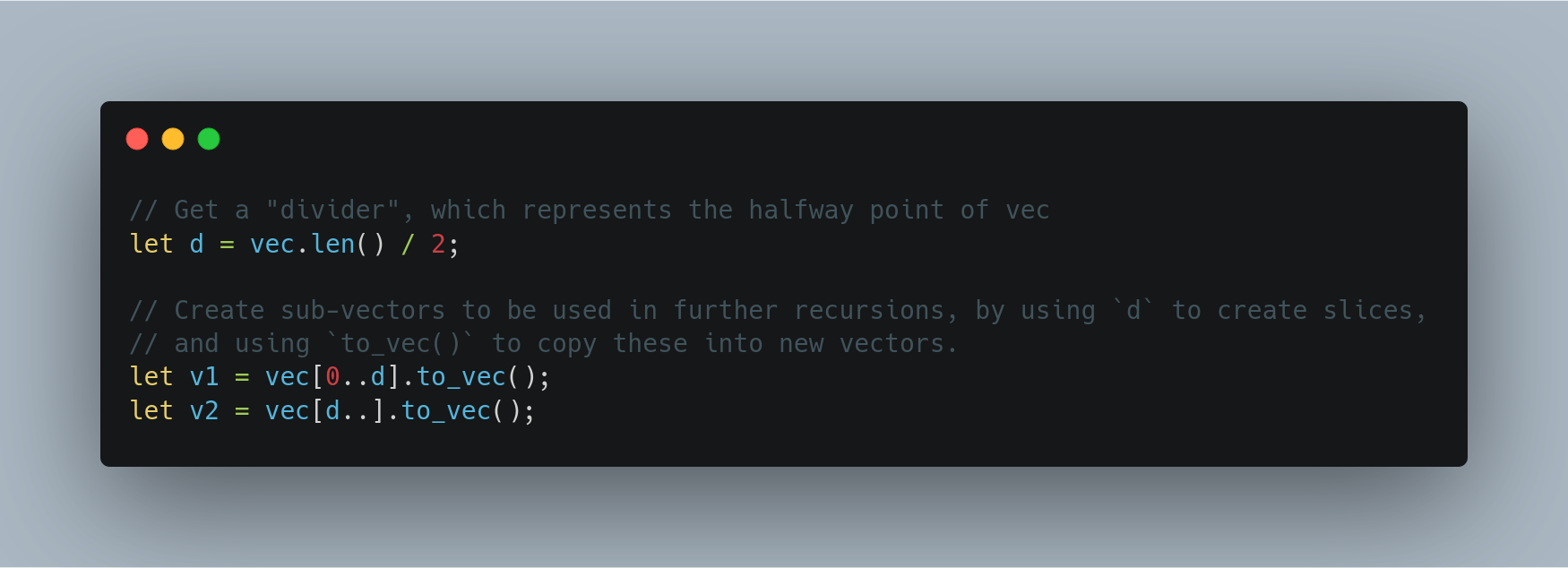
// Get a "divider", which represents the halfway point of vec
let d = vec.len() / 2;

// Create sub-vectors to be used in further recursions, by using `d` to create slices,
// and using `to_vec()` to copy these into new vectors.
let v1 = vec[0..d].to_vec();
let v2 = vec[d..].to_vec();

Изначально я преобразовал d в целое число, ожидая, что это приведет к типу с плавающей запятой, но это вызвало проблемы при использовании d в приведенных выше фрагментах, поскольку эта нотация предполагает тип, называемый типом usize. Оказывается, что без приведения приведенная выше операция деления также возвращает частное с типом usize, поэтому я могу использовать ее напрямую, как указано выше. Из моего ограниченного понимания, usize похож на целые числа, но их емкость полностью зависит от архитектуры компьютера (т.е. 32 против 64 бит), тогда как для таких типов, как u32 и u64, очевидно, есть заданные размеры.

Я буду копаться в этом в будущем - я заметил, что это широко используется в Rust и стандартной библиотеке, поэтому я предполагаю, что для этого есть причина, а не использование предсказуемых типов. Если у вас есть здесь полезные советы, напишите мне

Теперь, когда у нас есть «подвекторы», мы можем перейти к нашей функции сортировки. Синтаксис для этого такой, как ожидалось, хотя важно подчеркнуть, что в приведенном ниже примере эффективно заменяются несортированные v1 и v2 их отсортированными аналогами, полученными из merge_sort.

let v1 = merge_sort(v1);
let v2 = merge_sort(v2);

На этом этапе мы можем рассматривать v1 и v2 как отсортированные векторы, но нам все равно нужно объединить их в один вектор, чтобы этот конечный продукт также был отсортирован. Для начала я создал вектор с именем retvec, который изначально должен был быть пустым, но чтобы я вставлял в них значения при повторении v1 и v2.

let mut retvec = Vec::new();

То, что произошло потом, было действительно интересно. Этот синтаксис действительно действителен, но компилятор Rust недоволен этим утверждением; нам также нужно вставить значения в вектор, чего я в то время не удосужился сделать.

RUST_BACKTRACE=1 cargo run --example mergesort
   Compiling rust-algorithms v0.1.0 (/home/mierdin/Code/rust-algorithms)
error[E0282]: type annotations needed for `std::vec::Vec<T>`
  --> examples/mergesort.rs:34:21
   |
34 |   let mut retvec = Vec::new();
   |       ----------   ^^^^^^^^ cannot infer type for type parameter `T`
   |       |
   |       consider giving `retvec` the explicit type `std::vec::Vec<T>`, where the type parameter `T` is specified

Как только я продолжил свою реализацию и начал передавать значения в вектор, компилятор Rust перестал жаловаться, поскольку нажатие значения неявно сообщило Rust, что нам нужен определенный тип для этих векторных элементов (в данном случае целые числа из v1 и v2). Я мог бы также сделать то, что просил компилятор, и сам установить тип с помощью let mut retvec: Vec = Vec::new();, но краткая борьба здесь напомнила мне, что у меня была возможность быть более Расти.

Что мне нравится в Rust, так это то, что он побуждает вас механически сочувствовать, то есть работать с базовым оборудованием, а не против. Иногда это выполняется компилятором, иногда это настоятельно рекомендуется в соответствии с соглашением или инструментами, доступными на языке. Конечно, мы могли бы создать пустой вектор и «протолкнуть» его, когда у нас будет готово новое значение, но это часто может привести к крайне неэффективному распределению памяти. Вместо того, чтобы увеличивать вектор по одному значению за раз, в этом случае мы действительно точно знаем, насколько большим станет retvec: сумма длин v1 и v2!

  let size = v1.len() + v2.len();

С этим мы можем использовать vec! макрос для создания вектора с точным размером, который мы хотим. Это означает, что во время выполнения мы будем запрашивать выделение памяти для этого вектора только один раз, и этого выделения будет достаточно на протяжении всего времени существования этого вызова функции. Мы также передаем 0 этому макросу, чтобы предварительно заполнить каждый индекс значением 0, но мы перезапишем каждый из них соответствующими значениями во время слияния.

  let size = v1.len() + v2.len();
  let mut retvec = vec![0; size];

Обратите внимание, что мы также могли использовать Vec::with_capacity (size); для достижения той же цели. Если вы используете это, вам все равно нужно будет убедиться, что вы используете retvec.push() для передачи значений в вектор (который, опять же, также устанавливает тип для значений вектора). Вместо этого я решил предварительно заполнить нулями с помощью vec! макрос, и установить значения retvec через индекс, управляемый переменной счетчика. Кажется, что в любом случае все работает нормально, важно то, что мы заранее выполнили только одно выделение памяти.

Помните, что ключевым аспектом сортировки слиянием является то, что мы можем с уверенностью предположить, что v1 и v2 уже отсортированы к этому моменту. Именно благодаря этому факту мы можем выполнить простую логику слияния, описанную ниже. Поскольку мы знаем, что меньшие значения уже находятся в начале каждого вектора, мы просто просматриваем каждый, по одному индексу за раз. Мы берем меньшее из двух, увеличиваем соответствующий счетчик и добавляем это значение к следующему индексу retvec. В конце концов, ретвек тоже будет отсортирован.

while i < v1.len() && j < v2.len() {
  if v1[i] < v2[j] {
    retvec[k] = v1[i];
    i+=1;
  } else {
    retvec[k] = v2[j];
    j+=1;
  }
  k+=1;
}

Наконец, добавьте все оставшиеся значения. Фактически будет запущен только один из этих блоков (поскольку предыдущий цикл не завершился бы, если бы один из счетчиков не достиг длины соответствующего вектора). Кроме того, поскольку мы сравнивали значения в предыдущем цикле, мы можем с уверенностью предположить, что любой вектор, у которого есть оставшиеся значения для использования, сортируется, а также содержит значения, которые больше любого из другого вектора. Поэтому мы просто перебираем их и добавляем в retvec.

while i < v1.len() {
  retvec[k] = v1[i];
  i+=1;
  k+=1;
}
while j < v2.len() {
  retvec[k] = v2[j];
  j+=1;
  k+=1;
}

На этом этапе retvec должен представлять объединенный отсортированный вектор, который мы можем вернуть.

Реализация этого алгоритма дала мне реальный, Rust опыт работы с:

Тип usize
Рекурсия
Механически симпатичное распределение памяти

Вывод

Я не уверен, продолжу ли я эту серию, потому что у меня есть другие подпроекты, которые помогут мне глубже погрузиться не только в Rust, но и на другие темы. На данный момент это было действительно забавное введение, дающее мне реальный опыт работы с Rust и начало наращивания мышечной памяти. Я думаю, что многие из того, что заставляет людей уклоняться от новых языков, заключается в том, что они их еще не знают.

Мне все еще очень неудобно работать с Rust, но я знаю, что это потому, что язык для меня еще очень нов. Однако я чувствую себя намного увереннее, чем в начале года, и напоминаю себе, что я чувствовал то же самое в отношении Go и даже Python, когда начинал их изучать. Подобные примеры позволяют мне заставить себя избавиться от этого страха и начать знакомство, необходимое для действительно продуктивной работы. Для начала важно читать и смотреть видео, но в какой-то момент вам просто нужно начать пачкать руки.

Надеюсь, это было полезно и для вас!