Я получил своевременный поток данных в Rust и выполняю захватывающие вычисления! Я собираюсь объяснить один, который я считаю особенно крутым, и который я собираюсь попробовать использовать для некоторого анализа производительности базовой системы (система до сих пор подвергалась только микротестам задержки ...).

Код всего, о чем я расскажу, доступен в Интернете. Это пока не особенно красиво, но погоди.

Серьезно, вы действительно можете подождать. А пока вы можете прочитать этот отличный пост!

Реляционные соединения

Реляционное соединение - вещь довольно хорошо изученная, и я просто собираюсь дать здесь небольшое описание, чтобы у нас была общая терминология. Проблема начинается с набора отношений, мысленных таблиц; назовем эти отношения. Также есть несколько атрибутов, которые мы будем называть. Каждое отношение именует некоторое подмножество этих атрибутов, и каждый элемент в отношении имеет значение для каждого именованного атрибута. Не все отношения должны использовать один и тот же набор атрибутов.

Проблема реляционного соединения состоит в том, что для нескольких отношений определяется набор кортежей по всему пространству атрибутов, так что для каждого кортежа его проекция на атрибуты каждого отношения существует в этом отношении.

Пример

Рассмотрим первые записи трех отношений по трем атрибутам:

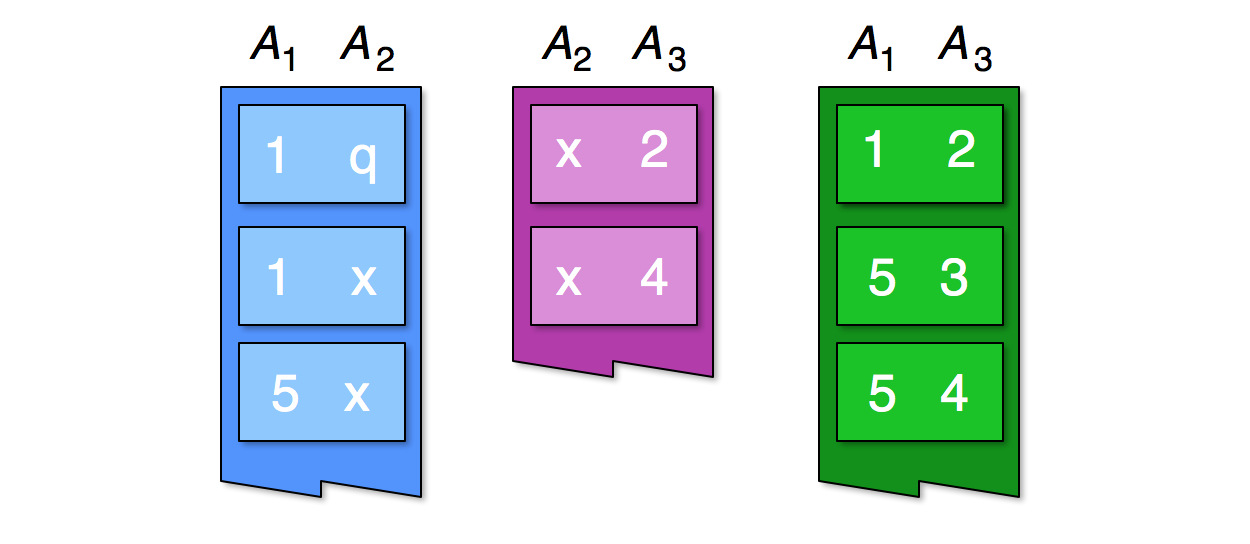
Мой полезный скриншот

Реляционное соединение между тремя отношениями должно содержать по крайней мере тройки и, поскольку мы можем видеть в первом отношении пары и, во втором отношении пары и, а в третьем отношении пары и.

Конечно, в полном соединении может быть больше записей, поскольку мы видим больше записей из каждого отношения.

Старые методологи

Есть много способов выполнить двоичное соединение между двумя отношениями, но самый простой - это хэш-соединение, когда вы просматриваете общие атрибуты между двумя отношениями и хешируете каждый кортеж в зависимости от их ограничения на эти атрибуты. Для каждой пары совпадающих кортежей (по одному от каждого отношения) вы формируете расширенный кортеж, который принимает объединение атрибутов отношений.

В приведенном выше примере мы могли бы объединить первые два отношения путем хеширования записей с помощью атрибута. Это соответствует и из первого отношения, и из второго отношения. Выходными данными в этом случае являются четыре тройки:,, и. Запись ничему не соответствует во втором отношении и не дает результата.

Чтобы выполнить многостороннее соединение, можно просто захватить отношения и присоединиться к ним, пока не будут использованы все отношения. Это дает правильный ответ, но может быть очень медленным. Более разумный способ - сформировать «план», который представляет собой двоичное дерево, в котором листья являются отношениями, а внутренние узлы соответствуют соединениям отношений. Корнем этого дерева является объединение всех отношений, но древовидная структура подсказывает, какие отношения лучше всего начать объединять.

В приведенном выше примере мы могли бы предпочесть объединить три отношения путем первого объединения и, что приведет к созданию только двух записей перед объединением с. Составление разумного плана присоединения - это то, о чем исследователи баз данных любят говорить на своих необычных встречах, и это хороший способ завязать разговор.

Более свежие работы

Реляционные соединения существуют так давно, что вы можете быть немного удивлены, узнав, что здесь все еще ведется новая работа. Вы можете быть еще более удивлены, узнав, что в некоторых отношениях люди довольно давно делали это неправильно. Это именно то, что наблюдают Нго и др. В потрясающей работе:

Стандартный подход к вычислению реляционных объединений, при котором один многократно выполняет двоичные объединения, может выполнять асимптотически больше работы, чем объединение могло бы когда-либо создавать выходные кортежи.

В примере трехстороннего соединения, если каждое отношение имеет размер, может быть не больше выходных кортежей, поскольку math. Однако существуют входные данные, так что любой план, основанный на бинарных соединениях, будет работать.
Существуют алгоритмы, которые никогда не выполняют больше работы (асимптотически), чем объединение могло бы для некоторых входных данных того же размера произвести выходные кортежи. Для трехстороннего соединения они будут выполнять вычисления.

Этот второй пункт не означает, что они будут выполнять ровно столько работы, сколько они будут создавать выходные кортежи, а только то, что, когда они выполняют много работы, у них, по крайней мере, есть оправдание, что они, возможно, должны были это сделать.

Вы знаете, у кого нет даже такого оправдания? Стандартные подходы к вычислению реляционных объединений.

Общее соединение

Алгоритм, который подробно описывают Нго и др., На самом деле довольно общий. Они даже называют алгоритм GenericJoin.

Я собираюсь сосредоточиться на конкретной реализации этого. Я должен сказать здесь, что конкретное осознание произошло благодаря другим людям, а не мне. Я не совсем уверен, кто заслуживает доверия, но Семих Салихоглу и Крис Ре - те, кто научил меня обработке соединений в наихудшем случае, и именно с Семих, Крисом и Майклом Айсардом мы разработали первую версию этого в Наяда.

Конкретное соединение

Вместо того, чтобы думать о добавлении отношений по одному, как при классической обработке соединений, мы будем думать о добавлении атрибутов по одному.

Представьте, что у нас есть соединение по атрибутам, и мы хотим вывести соединение по атрибутам. Для каждого мы хотим создать набор поддерживаемых каждым отношением.

Самый простой способ сделать это - просто спросить каждого: «Какие расширения вы поддерживаете?» Для каждого мы пересекаем их результаты и возвращаемся для каждого на пересечении.

Конечно, чтобы запросить отношения для расширений и быстро получить ответ, каждое отношение необходимо проиндексировать по каждому префиксу атрибутов. Это вводит избыточность, но мы собираемся с ней работать.

Умное объединение

В этом алгоритме пока нет ничего разумного, но Нго и др. Наблюдают, что если вы сделаете это пересечение осторожно, вы получите алгоритм оптимального соединения наихудшего случая. Особое внимание, которое вы должны проявить к каждому из них, заключается в том, чтобы выполнять работу только пропорционально наименьшему набору возможных расширений из любого отношения. Вместо того, чтобы просто пересекать все волей-неволей, мы должны начать с самого малого и продвигаться вверх.

К счастью, вычисление пересечения небольшого набора с большим набором - это то, что может занять время, примерно линейное по размеру меньшего набора. Вы можете либо хешировать все повсюду, либо использовать логарифмический коэффициент (они согласны с этим), используя различные методы двоичного поиска.

Но давайте посмотрим на секунду и убедимся, что мы это понимаем. Для каждого из них мы должны попросить зависящее от данных отношение предложить некоторые расширения, а затем попросить другие отношения подтвердить их. Не существует статичного плана «сначала все спрашивают, потом…»; мы собираемся обмениваться ими повсюду, вместо того, чтобы передавать записи через отношения, как при традиционном плане объединения.

«Обмен», говорите вы? Надеюсь, вы понимаете, к чему все идет.

Реализация на Rust

Очевидно, мы собирались это сделать. Не удивляйся.

Некоторые абстракции

Действительно ли нам нужны отношения и кортежи повсюду в нашем коде? Нет! Давайте займемся абстракцией.

Из приведенного выше обсуждения мы видим, что нам действительно нужно лишь несколько вещей из отношения:

Он должен иметь возможность сообщать, сколько расширений он предлагает.
Он должен иметь возможность предлагать конкретные расширения для.
Он должен иметь возможность пересекать предлагаемые расширения со своими расширениями.

Итак, давайте напишем трэйту, которая делает это. Я назову задачи выше «подсчитать», «предложить» и «пересечь».

pub trait PrefixExtender<Prefix, Extension> {
    fn count(&self, &Prefix) -> u64;
    fn propose(&self, &Prefix) -> Vec<Extension>;
    fn intersect(&self, &Prefix, &mut Vec<Extension>);
}

Я думаю, это как и было обещано. Это то, что необходимо реализовать в отношении, чтобы мы могли расширить элемент типа Prefix (think кортежи) с помощью элемента типа Extension (think).

Распределенная реализация

Конечно, мы действительно хотели бы расширить каждый из префиксов параллельно для множества рабочих процессов. По крайней мере, я этого хочу. Если вам все равно, вы должны полностью пропустить эту часть.

Чтобы это произошло, я собираюсь использовать библиотеку своевременных потоков данных, которая использует тип Stream <G, Prefix> для представления распределенного потока записей типа Prefix. Параметр типа G описывает, как распределяется поток и как будут выполняться вычисления, и пока мы просто проигнорируем его.

Нам нужно поднять реализацию PrefixExtender <P, E> для работы с потоками Stream <G, P>. К счастью, я собираюсь сделать это за нас, реализовав следующий трейт для любого типа, реализующего PrefixExtender <P, E> (плюс некоторая информация о том, как распределять префиксы среди рабочих).

pub trait StreamPrefixExtender<G, P, E> {
    fn count(&self, &mut Stream<G, (P, u64, u64)>, u64) -> Stream<G, (P, u64, u64)>;
    fn propose(&self, &mut Stream<G, P>) -> Stream<G, (P, Vec<E>)>;
    fn intersect(&self, &mut Stream<G, (P, Vec<E>)>) -> Stream<G, (P, Vec<E>)>;
}

Записи несут с собой больше информации; информация, которая раньше была в стеке, теперь должна быть помещена в сами записи. Например, мы указываем отношение с наименьшим счетом тройкой (префикс: P, счетчик: u64, индекс: u64), данные, которые в противном случае были бы в локальных переменных. Сигнатура счетчика также изменяется, чтобы принимать и производить тройки, как при обновлении переменных стека.

Хотя мы собираемся использовать этот интерфейс, вам не нужно много об этом знать. Главное, что нужно знать, это то, что существует около пятидесяти довольно предсказуемых строк кода, которые реализуют StreamPrefixExtender <G, P, E> для любого типа, реализующего PrefixExtender <P, E>.

impl<G, P, E, PE> StreamPrefixExtender<G, P, E> for Rc<RefCell<PE>>
where PE: PrefixExtender<P, E> {
    // the library does this for you, you just implement PrefixExtender.
}

Технически говоря, вам также нужно будет своевременно сообщить потоку данных, как распределять префиксы. Это будет зависеть от того, как вы распространяете свои отношения, и об этом я расскажу подробнее в одном из следующих постов.

Конкретное объединение в Rust

С этими абстракциями мы теперь готовы построить слой конкретного алгоритма соединения. Прежде чем мы это сделаем, давайте посмотрим, что это будет значить.

pub trait SpecificJoinExt<G, P, E> {
    fn extend(&mut self, extenders: Vec<Box<StreamPrefixExtender<G, P, E>>>)
        -> Stream<G, (P, Vec<E>)>;
}

Нам нужно написать метод для Stream <G, P>, который с учетом вектора произвольных вещей, реализующих трэйт StreamPrefixExtender <G, P, E>, генерирует поток пар (P, Vec). Кроме того, мы должны делать это с умом, описанным выше, иначе мы будем работать медленно, как все скрипучие системы баз данных.

Я просто покажу вам код, но комментарии должны вас проинформировать. Все как мы сказали.

impl<G, P, E> SpecificJoinExt<G, P, E> for Stream<G, P> {
    fn extend(&mut self, extenders: Vec<Box<StreamPrefixExtender<G, P, E>>>)
            -> Stream<G, (P, Vec<E>)> {

        // start with horrible proposals from a non-relation
        // ask each extender to try to improve each proposal
        let mut counts = self.select(|p| (p, 1 << 63, 1 << 63));
        for index in (0..extenders.len()) {
            counts = extenders[index].count(&mut counts, index as u64);
        }

        // for each of the extenders ...
        let mut results = Stream::empty();
        for index in (0..extenders.len()) {
            // find the prefixes the extender "won" the right to extend
            let mut nominations = counts.filter(move |p| p.2 == index as u64)
                                        .select(|(x, _, _)| x);

            // get the extensions and ask each other extender to validate
            let mut extensions = extenders[index].propose(&mut nominations);
            for other in (0..extenders.len()).filter(|&x| x != index) {
                extensions = extenders[other].intersect(&mut extensions);
            }

            // fold surviving extensions into the output
            results = results.concat(&mut extensions);
        }

        return results;
    }
}

В этом весь алгоритм. Это действительно не очень сложно. Скорее, это один уровень алгоритма. Чтобы заполнить полное реляционное соединение, нам нужно вызывать расширение несколько раз, с разными объектами PrefixExtender, которые обертывают одни и те же отношения, только для разной длины префикса. Приведем пример.

Перечислитель треугольников с малой задержкой

Если мы определяем граф как набор пар (src, dst), треугольник определяется как тройка (a, b, c), где (a, b), (b, c) и (a, c) - каждый в наборе пар. Мы можем думать о запросе треугольников как о реляционном соединении трех отношений, которые представляют собой одни и те же данные, только привязанные к разным парам атрибутов.

Определение PrefixExtender

Мы представим фрагмент графа списком назначений и смещений в этот список для каждой вершины. Для каждого интервала мы будем отсортировать пункты назначения, чтобы упростить проверку пересечений.

pub struct GraphFragment<E: Ord> {
    nodes: Vec<usize>,
    edges: Vec<E>,
}

Мы просто напишем быструю вспомогательную функцию, позволяющую использовать get на краях, связанных с узлом:

impl<E: Ord> GraphFragment<E> {
    fn edges(&self, node: usize) -> &[E] {
        if node + 1 < self.nodes.len() {
            &self.edges[self.nodes[node]..self.nodes[node+1]]
        }
        else { &[] }
    }
}

Стоит отметить, что Rust делает здесь несколько очень умных вещей. Он замечает, что мы возвращаем ссылку на некоторую память типа &[E], и единственное, на что она может ссылаться, - это &self. Затем Rust устанавливает ограничение времени жизни для вывода как &self и гарантирует, что, когда мы используем результат, ему не разрешено переживать себя.

Я собираюсь немного соврать и представить упрощенный набросок PrefixExtender для GraphFragment. В упрощенной версии используется GraphFragment с подсчетом ссылок, все это Rc <RefCell <... >>. Это позволяет нам иметь только одну загруженную копию графика и делиться ею между людьми, которые в ней нуждаются. Нам также понадобится вспомогательная функция типа L: Fn (& P) -> u64 для извлечения идентификатора узла из типа P.

impl<P, E, L> PrefixExtender<P, E> for (Rc<RefCell<GraphFragment<E>>>, L)
where E: Ord, L: Fn(&P)->u64 {
    // counting is just looking up the edges
    fn count(&self, prefix: &P) -> u64 {
        let &(ref graph, ref logic) = self;
        let node = logic(&prev.0) as usize;
        graph.borrow().edges(node).len() as u64
    }

    // proposing is just reporting the slice back
    fn propose(&self, prefix: &P) -> Vec<E> {
        let &(ref graph, ref logic) = self;
        let node = logic(prefix) as usize;
        graph.borrow().edges(node).to_vec()
    }

    // intersection 'gallops' through a sorted list to find matches
    // what is "galloping", you ask? details coming in just a moment
    fn intersect(&self, prefix: &P, list: &mut Vec<E>) {
        let &(ref graph, ref logic) = self;
        let node = logic(prefix) as usize;
        let mut slice = graph.borrow().edges(node);
        list.retain(move |value| {
            slice = gallop(slice, value); // skips past elements < value
            slice.len() > 0 && &slice[0] == value
        });
    }
}

Это было довольно просто, да? Конечно, до того, как я написал этот вспомогательный метод Edge (node), все было намного сложнее. Также немного грустнее, когда я не лгу о том, как все работает, но давайте не будем допустить, чтобы это встало между нами.

В интересах полноты (и для того, чтобы не упустить мой код), давайте посмотрим на реализацию gallop. От входного среза и значения он перескакивает вперед с экспоненциально увеличивающимися шагами, а затем, как только он превысит целевое значение, он продвигается вперед с экспоненциально уменьшающимися шагами.

// advances slice to the first element not less than value.
pub fn gallop<'a, T: Ord>(mut slice: &'a [T], value: &T) -> &'a [T] {
    if slice.len() > 0 && &slice[0] < value {
        let mut step = 1;
        while step < slice.len() && &slice[step] < value {
            slice = &slice[step..];
            step = step << 1;
        }

        step = step >> 1;
        while step > 0 {
            if step < slice.len() && &slice[step] < value {
                slice = &slice[step..];
            }
            step = step >> 1;
        }

        &slice[1..]   // this shouldn't explode... right?
    }
    else { slice }
}

Метод gallop может использовать любой фрагмент в качестве входных данных, и мы даем ему фрагмент, вырезанный из списка ребер графа. Если мы неправильно используем срез результата, может возникнуть ужасный риск сглаживания, скачка данных, де- или перераспределения. Rust может подтвердить, что ничего из этого не происходит, и просто позволяет нам использовать ту же самую память. Это достигается за счет закрытия удержания, написанного мною метода (галоп) и множества странных логик. Отлично!

Построение запроса треугольников

Итак, напомним, у нас есть реализация PrefixExtender <P, E> всякий раз, когда у нас есть комбинация GraphFragment и L: Fn (&P) -> u64. Эта вторая часть, функция, сообщает нам, как превратить префикс P в целое число, которое мы можем использовать для поиска расширений на графике. Мы везде используем одни и те же данные графа, но имитируем множественные отношения, позволяя функции от префикса к атрибуту варьироваться.

При этом давайте посчитаем несколько треугольников! Мы будем делать это по частям. Я снова немного совру и представлю несколько упрощений. Ничего ужасного, просто возможно загадочные вещи, которые потребуют отвлечения внимания для рационализации (и, возможно, просто плохой дизайн с моей стороны).

Сначала мы просто пишем код, который из Коммуникатора, который указывает индекс рабочего и количество его пиров, выясняет, какой фрагмент графа этот рабочий будет загружать и за который будет отвечать. Затем код подготавливает вычисление потока данных и ввод, в который мы будем вводить значения a: u32. Все это - шаблон своевременного потока данных, и это не очень интересно с алгоритмической точки зрения.

fn triangles<C, F>(communicator: C, graph_source: F)
where C: Communicator,
      F: Fn(u64,u64)->GraphFragment<u32> {

    // load up the slice of graph corresponding to our index out of peers.
    let graph = graph_source(communicator.index(), communicator.peers());
    let graph = Rc::new(RefCell::new(graph));

    // prepare a new computation with one input.
    let mut computation = new_computation(communicator);
    let (mut input, mut stream) = computation.new_input();

Следующим шагом будет создание расширителя от a до (a, b). Нам просто нужно связать копию графика с функцией, которая преобразует a в идентификатор узла графа, и она предложит соседние значения b.

//  // define an extender that uses 'a' to suggest x: '(a,x)' extensions
    let ext_b = vec![Box::new((graph.clone(), |&a| { a as u64 }))];
    let mut pairs = stream.extend(ext_b).flatten();

Этот метод flatten() просто преобразует Stream <G, (P, Vec)> в Stream <G, (P, E)>. Это где-то всего 17 строк кода, так что ура, чтобы своевременный поток данных был прост в использовании (по крайней мере, кратко).

Следующим шагом будет создание расширителей от пар (a, b) до троек ((a, b), c). Будет два расширителя, так как мы хотим, чтобы значения c были такими, чтобы оба (a, c) и (b, c) присутствовали на графике. Каждый расширитель должен взять (a, b) и идентифицировать источник края, и есть только два варианта.

//  // define extenders using 'a' and 'b' to suggest x: (a,x) and x:(b,x)
    let ext_c = vec![Box::new((graph.clone(), |&(a,_)| { a as u64 })),
                     Box::new((graph.clone(), |&(_,b)| { b as u64 }))]

    let mut triangles = pairs.extend(ext_c).flatten();

Давайте также посмотрим на то, что мы видим, распечатав треугольники (обратите внимание на еще 16 строк кода).

//  // take a peek at what gets produced.
    triangles.observe(|&tri| println!("triangle: {:?}", tri));

Ok, we’ve got the data loaded up, the computation defined, and are ready to go. Let’s triangularate!

//  // finalize dataflow structure
    computation.0.borrow_mut().get_internal_summary();
    computation.0.borrow_mut().set_external_summary(Vec::new(), &mut Vec::new());

    // introduce u32s to find triangles rooted from them
    for node in (0..graph.borrow().nodes.len()) {
        input.send_messages(&((), node as u64), vec![node as u32]);
        input.advance(&((), node as u64), &((), node as u64 + 1));
        computation.0.borrow_mut().step();
    }

    // close input and finish any computation
    input.close_at(&((), graph.borrow().nodes.len() as u64));
    while computation.0.borrow_mut().step() { }
}

Это проходит через каждый возможный исходный узел и создает все треугольники, начиная с этой вершины.

Разве вы не сказали «низкая задержка»?

Хорошая точка зрения. Хотя мы прошли все узлы по порядку, чтобы перечислить все треугольники, нам это не потребовалось. Мы могли бы так же легко написать основной цикл, как:

for epoch in (0..) {
    let node = read_u32_from_console(); // not a real function!
    input.send_messages(&((), epoch), vec![node]);
    input.advance(&((), epoch), &((), epoch + 1));
    computation.0.borrow_mut().step();
}

Это считывает ввод от пользователя, запускает его в поток данных, который распечатывает наблюдаемые треугольники как можно скорее. Чтобы понять, насколько быстро, давайте включим таймер в стандартном цикле выше и запустим процесс в однопоточном режиме на довольно стандартном наборе данных LiveJournal:

Предостережение: код практически не протестирован и может ошибаться; не покупайте / не продавайте ничего на основании этих данных.

enumerated triangles from (0..1) in 67947ns
enumerated triangles from (1..2) in 42738ns
enumerated triangles from (2..3) in 26064ns
enumerated triangles from (3..4) in 48006ns
enumerated triangles from (4..5) in 19921ns
...

Таким образом, время между введением идентификатора узла и возвращением всех треугольников составляет несколько десятков микросекунд. Эти числа немного улучшаются с пакетированием, сокращая некоторые накладные расходы:

enumerated triangles from (0..10) in 231301ns
enumerated triangles from (10..20) in 276721ns
enumerated triangles from (20..30) in 149940ns
enumerated triangles from (30..40) in 137285ns
enumerated triangles from (40..50) in 155781ns
...

И даже лучше с еще большим количеством пакетов, так как он начинает больше походить на 10-15 мкс амортизированных на вершину.

enumerated triangles from (0..1000) in 10129064ns
enumerated triangles from (1000..2000) in 12018695ns
enumerated triangles from (2000..3000) in 11323832ns
enumerated triangles from (3000..4000) in 11224684ns
enumerated triangles from (4000..5000) in 14810182ns
...

Эта программа предназначена для выявления нескольких компонентов и выявления того, что работает медленно и требует некоторой доработки. Базовая система все еще имеет много возможностей для улучшения (я думаю). Цифры должны только улучшаться.

Треугольники такие уж отстойные.

Треугольники такие 2014! Все делают треугольники! Сделайте что-нибудь круче!

// define extenders to add a 'd' coordinate connected to each of a, b, c.
let ext_d = vec![Box::new((graph.clone(), |&((a,_),_)| { a as u64 })),
                 Box::new((graph.clone(), |&((_,b),_)| { b as u64 })),
                 Box::new((graph.clone(), |&((_,_),c)| { c as u64 }))];

let mut quads = triangles.extend(ext_d).flatten();

Если вы пропустили это, мы определяли вычисление потока данных для перечисления 4-х кликов.

enumerated 4-cliques from (0..1) in 164474ns
enumerated 4-cliques from (1..2) in 230093ns
enumerated 4-cliques from (2..3) in 40667ns
enumerated 4-cliques from (3..4) in 154921ns
enumerated 4-cliques from (4..5) in 67344ns
...

Не впечатлен? Как насчет:

enumerated 5-cliques from (0..1) in 115570ns
enumerated 5-cliques from (1..2) in 311967ns
enumerated 5-cliques from (2..3) in 110915ns
enumerated 5-cliques from (3..4) in 126838ns
enumerated 5-cliques from (4..5) in 104806ns
...

Как насчет:

enumerated 6-cliques from (0..1) in 107292ns
enumerated 6-cliques from (1..2) in 342537ns
enumerated 6-cliques from (2..3) in 93778ns
enumerated 6-cliques from (3..4) in 134948ns
enumerated 6-cliques from (4..5) in 87148ns
...

Я могу продолжать (серьезно, я написал программу для этого).

Поиск мотивов произвольного графа (маленькие подграфы, которые вы хотите найти в большом графе) действительно легко написать. Я уверен, что есть много более разумных исследований о том, как это сделать, но, по крайней мере, это оптимально в худшем случае.

Заворачивать

В совместных исследованиях ведется серьезная классная работа. Он совсем не такой устаревший, как я думал. Но, что важно, эти новые алгоритмы нуждаются в более совершенных системах, чем ваши стандартные пакетные процессоры.

Сколько ваших любимых графических процессоров способны начать обработку 6 кликов менее чем за миллисекунду, при этом объем памяти, примерно равный самому графу? Не тот, которым пользуетесь? Почему нет? Плохие вещи перестали быть крутыми в старшей школе ...

С положительной стороны, в дополнение к этому коду, Naiad может все это делать, и Flink тоже должен это делать.

С моей точки зрения, теперь у меня есть классная проблема, которую я могу использовать для настройки своевременного потока данных. Я ожидал, что он станет лучше и удобнее (и, вероятно, сейчас я тоже попробую его в большем количестве конфигураций).

Сноска: перекос

Одна из теоретических проблем, связанных с подобным подходом, заключается в том, насколько хорошо он распределяется при наличии перекоса. Каждый из наших операторов подсчета, предложения и пересечения является «параллельным с данными», но действительно ли это полезно, когда сами данные неравномерно распределяются между рабочими.

Реализация, о которой я говорил, не является устойчивой к перекосам. Если вершина имеет действительно высокую степень, все ребра могут быть размещены на одной машине. Добавление большего количества машин не приведет к ускорению предложения и не предотвратит отправку всех предложений на этот единственный механизм для пересечения.

Однако вы можете скомпоновать устойчивую версию каждой из этих операций.

count, естественно, устойчив к перекосам, потому что нам просто нужно число для каждого префикса. Они могут быть распределены (равномерно) с помощью хеша на префиксе.
propose можно сделать асимметричным путем распространения расширений для каждого префикса на машины последовательно с машины, идентифицированной хешем префикса. Нам нужно знать, сколько машин запрашивать продление, но каждое предложение должно сопровождаться подсчетом (я его отбросил; упс).
Пересечение можно сделать асимметричным путем распределения записей (P, E) по хешам и доставки предложений в известное место для каждого отношения.

Я недостаточно разбираюсь в работе в этой области, чтобы точно знать, что это соответствует всем желаемым параметрам. Например, желательно, чтобы вычисления занимали несколько «циклов» в смысле MapReduce. Учитывая, что я не использую MapReduce и все еще выполняю вычисления, меня это не особо беспокоит.

Отбросив комментарии в сторону, было бы хорошо понять, действительно ли этот подход представляет собой масштабируемый, устойчивый к перекосам алгоритм оптимального соединения в худшем случае. Мне сказали, что это было бы круто.

Кредиты и текущая работа

Эта область (оптимальная обработка соединений в наихудшем случае) очень крутая, и я в долгу перед Семихом Салихоглу и Крисом Ре за то, что они представили нас двоих. Эти люди и их коллеги по-прежнему очень активны, раздвигая границы того, что можно сделать, чтобы ускорить и ускорить обработку соединений.

У Семи, Криса и других есть подход, позволяющий сделать еще более сложные соединения эффективными с помощью декомпозиции запросов по гипердереву. «Древовидные» ациклические запросы знают способы их оптимальной обработки (в стиле Витерби). Как только вы получаете циклы, они ломаются, но если вы можете разложить запрос на дерево небольших циклических запросов и использовать наихудшие оптимальные методы для циклических запросов, вы получите хорошие результаты.

У Криса Абергера, Криса и других есть изящный способ сделать тестирование пересечений намного более эффективным с помощью инструкций SIMD и показать, что они могут получить ускорение на порядки, используя эти методы. Различные «неназванные» проприетарные поставщики, кажется, выздоравливают и полностью проигрывают.

Есть много других работ, с которыми я не так хорошо знаком (пока), но, похоже, они продолжают появляться. Быть возбужденным!